
Microsoft Excel является одной из самых популярных программ для работы с таблицами и данными. Она предлагает широкий спектр функций, которые позволяют проводить сложные вычисления и анализировать большие объемы информации. В этой статье мы рассмотрим, как использовать вложенные функции в Excel для расчета статистических показателей.
Вложенные функции в Excel — это функции, которые содержатся внутри других функций. Это позволяет нам выполнять несколько операций одновременно и получать более точные результаты. Например, мы можем использовать вложенные функции для расчета среднего значения определенного диапазона ячеек, которые удовлетворяют определенному условию. Такие функции часто используются в статистике и экономических расчетах.
Одной из наиболее полезных вложенных функций в Excel является функция СУММЭСЛИ. Она позволяет нам вычислить сумму ячеек, которые удовлетворяют определенному условию. Например, мы можем использовать эту функцию для расчета суммы продаж определенного товара в определенный период времени. Внутри функции СУММЭСЛИ мы можем использовать другие функции, такие как функция СУММ или функция СРЗНАЧ, чтобы получить более точные результаты.
Внедрение вложенных функций в Excel может значительно упростить и ускорить вашу работу с данными. Благодаря им вы сможете проводить сложные анализы и расчеты статистических показателей, не прибегая к использованию сложных формул или макросов. Не бойтесь экспериментировать и пробовать различные комбинации вложенных функций, чтобы получить наилучшие результаты для вашей работы.
Что такое вложенные функции в Excel?
Вложенные функции в Excel позволяют учитывать множество факторов и создавать формулы с различными условиями и операциями, что делает их гибкими и мощными инструментами для обработки данных. Например, можно использовать вложенные функции для вычисления среднего значения только для определенного набора данных или для выполнения логических операций с условиями. В результате, пользователи могут получать более точные и подробные статистические показатели, основанные на определенных критериях и условиях.
Зачем использовать вложенные функции для расчета статистических показателей?
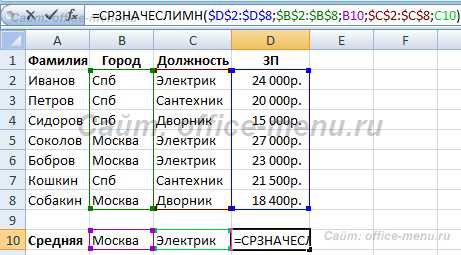

При работе с большим объемом данных и необходимостью проведения сложных расчетов статистических показателей, использование вложенных функций в Excel становится необходимым инструментом. Вложенные функции позволяют комбинировать несколько функций в одной ячейке для получения более точных и детализированных результатов.
Вложенные функции обеспечивают гибкость и удобство при работе со сложными формулами. Они позволяют производить несколько последовательных операций в рамках одной ячейки, используя результаты предыдущих расчетов для новых вычислений. Такой подход позволяет сэкономить время и упростить процесс обработки данных, особенно при работе с большими объемами информации.
Вложенные функции позволяют выполнять различные статистические расчеты, такие как подсчет среднего значения, медианы, стандартного отклонения и других показателей. Комбинируя различные функции, можно получить более полную картину и точные результаты исследуемых данных.
Также использование вложенных функций позволяет автоматизировать расчеты и обновлять результаты в реальном времени при изменении входных данных. Это особенно полезно при работе с динамическими наборами данных или при необходимости проведения регулярных обновлений.
Раздел 2: Примеры использования вложенных функций для расчета средних показателей
Использование вложенных функций в Excel позволяет эффективно расчитывать средние показатели для анализа данных. В данном разделе мы рассмотрим несколько примеров использования вложенных функций для расчета средних значений.
Пример 1: Расчет среднего значения стоимости продукции
Представим, что у нас есть таблица с данными о различных продуктах и их стоимости. Мы хотим вычислить среднюю стоимость продукции на основе этих данных.
| Название продукта | Стоимость (в рублях) |
|---|---|
| Продукт A | 100 |
| Продукт B | 200 |
| Продукт C | 150 |
Для расчета средней стоимости продукции мы можем использовать вложенную функцию «СРЗНАЧ», которая позволяет нам указать диапазон ячеек со значениями стоимостей продукции. Например, функция может выглядеть следующим образом:
=СРЗНАЧ(B2:B4)
Эта функция будет возвращать среднее значение стоимости продукции для указанного диапазона ячеек.
Пример 2: Расчет среднего значения количества продаж
Допустим, у нас есть таблица с данными о продажах товаров за определенный период времени. Мы хотим вычислить среднее значение количества продаж на основе этих данных.
| Название товара | Количество продаж |
|---|---|
| Товар A | 10 |
| Товар B | 15 |
| Товар C | 20 |
Для расчета среднего значения количества продаж мы также можем использовать функцию «СРЗНАЧ». Например:
=СРЗНАЧ(B2:B4)
Эта функция вернет среднее значение количества продаж для указанного диапазона ячеек.
В обоих примерах использования вложенных функций мы можем оперделить средние показатели, основываясь на данных из таблицы. Это позволяет нам легко и эффективно анализировать данные и получать нужную информацию.
Как использовать вложенные функции для расчета среднего арифметического?
Для расчета среднего арифметического в Excel можно использовать вложенные функции, которые позволяют комбинировать несколько функций в одной ячейке, чтобы получить итоговый результат.
Вложенные функции — это использование одной функции внутри другой функции. Например, для расчета среднего значения набора чисел, можно использовать функцию «СРЗНАЧ», внутри которой будет применяться функция «СУММ» для сложения чисел и функция «СЧЕТ» для подсчета количества чисел.
Пример формулы с вложенными функциями для расчета среднего арифметического выглядит следующим образом:
| Ячейка A1: | 10 |
| Ячейка A2: | 15 |
| Ячейка A3: | 20 |
| Ячейка B1: | =СРЗНАЧ(A1:A3) |
В данном примере в ячейке B1 используется функция «СРЗНАЧ», внутри которой указан диапазон ячеек A1:A3. Таким образом, функция «СРЗНАЧ» будет вычислять среднее значение чисел из этого диапазона (10, 15, 20) и возвращать результат 15.
Использование вложенных функций в Excel позволяет упростить и автоматизировать расчеты, обеспечивая точные и надежные результаты. Это полезный инструмент для работы с большими объемами данных и повышения эффективности работы.
Как использовать вложенные функции для расчета среднего геометрического?
Для расчета среднего геометрического в Excel можно использовать комбинацию вложенных функций, таких как POWER и AVERAGE. Функция POWER позволяет возвести каждое число в наборе в определенную степень, а функция AVERAGE вычисляет среднее значение полученных результатов.
Программа Excel позволяет вам создать формулу, которая сначала возведет каждое число в наборе в определенную степень, а затем найдет среднее значение полученных результатов. Для этого вам понадобится использовать вложенные функции POWER и AVERAGE. Функция POWER возводит каждое число в наборе в определенную степень, а функция AVERAGE находит среднее значение полученных результатов.
Например, чтобы найти среднее геометрическое для чисел 2, 4 и 8, вы можете использовать следующую формулу: =AVERAGE(POWER(2,1), POWER(4,1), POWER(8,1)). При выполнении этой формулы Excel сначала возведет число 2 в степень 1, затем число 4 в степень 1 и, наконец, число 8 в степень 1. Затем программа найдет среднее значение полученных результатов, которым будет являться искомое среднее геометрическое.
Раздел 3: Примеры использования вложенных функций для расчета дисперсии и стандартного отклонения
В Excel существует возможность использовать вложенные функции для расчета дисперсии и стандартного отклонения. Это позволяет более гибко и эффективно анализировать данные и получать точные статистические показатели.
Дисперсия — это мера разброса значений вокруг среднего значения. Для расчета дисперсии можно использовать функцию VAR.S, которая позволяет учесть все значения в выборке. К примеру, можно вычислить дисперсию для набора данных, представленного в виде столбца, используя следующую формулу: =VAR.S(A1:A10), где A1:A10 — диапазон данных.
Стандартное отклонение — это мера разброса значений в выборке. Для расчета стандартного отклонения можно использовать функцию STDEV.S, которая опирается на все значения в выборке. Например, для вычисления стандартного отклонения для того же столбца данных из предыдущего примера, можно использовать формулу =STDEV.S(A1:A10).
Использование вложенных функций позволяет автоматизировать расчет статистических показателей в Excel и получать точные результаты. Это удобно для анализа больших объемов данных и позволяет получить ценную информацию для принятия решений.
Ниже представлен пример таблицы, в которой использованы вложенные функции для расчета дисперсии и стандартного отклонения:
| № | Значение |
|---|---|
| 1 | 10 |
| 2 | 15 |
| 3 | 12 |
| 4 | 8 |
| 5 | 14 |
Для расчета дисперсии и стандартного отклонения в данной таблице можно использовать следующие формулы:
- Дисперсия:
=VAR.S(A2:A6) - Стандартное отклонение:
=STDEV.S(A2:A6)
Таким образом, с использованием вложенных функций в Excel можно легко и удобно рассчитать дисперсию и стандартное отклонение для анализа данных и принятия обоснованных решений.
Вопрос-ответ:
Можно ли использовать вложенные функции для расчета дисперсии и стандартного отклонения в других языках программирования?
Да, вложенные функции могут быть использованы для расчета дисперсии и стандартного отклонения в других языках программирования. Вложенные функции являются частью функционального программирования и позволяют определить функцию внутри другой функции. Это может быть полезно для создания компактного и поддерживаемого кода, а также для ограничения области видимости переменных. Примером другого языка программирования, где можно использовать вложенные функции, является JavaScript.
Как используются вложенные функции для расчета дисперсии и стандартного отклонения?
Вложенные функции в данном контексте используются для выполнения последовательных вычислений, которые включают в себя расчет дисперсии и стандартного отклонения. Вложенные функции могут быть определены внутри основной функции и использоваться для выполнения промежуточных шагов при расчете этих статистических показателей.
Как рассчитать дисперсию с использованием вложенных функций?
Для расчета дисперсии с использованием вложенных функций, нужно сначала вычислить среднее значение элементов выборки. Затем, определить внутреннюю функцию, которая будет принимать это среднее значение в качестве аргумента и использовать его для вычисления суммы квадратов разницы каждого элемента выборки с этим средним значением. Результатом выполнения вложенной функции будет сумма квадратов разницы. В основной функции, дисперсия будет получаться делением этой суммы на количество элементов выборки.
Как рассчитать стандартное отклонение с использованием вложенных функций?
Для расчета стандартного отклонения с использованием вложенных функций, нужно сначала рассчитать дисперсию с помощью вышеописанных шагов. Затем, внутри основной функции, определить еще одну вложенную функцию, принимающую значение дисперсии в качестве аргумента и возвращающую квадратный корень из этого значения. Результатом выполнения основной функции будет стандартное отклонение, которое будет равно значению этой вложенной функции.