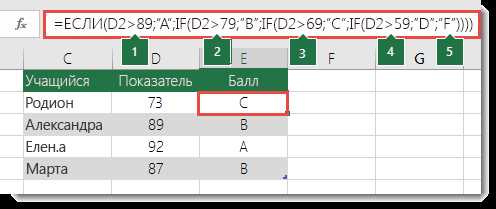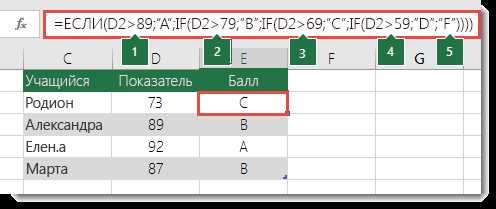

Excel предлагает множество функций, которые позволяют вам проводить различные вычисления и анализировать данные. Однако иногда возникают ситуации, когда вам необходимо объединить несколько функций в одной формуле. Именно для этого в Excel имеется возможность использовать вложенные функции.
Вложенные функции позволяют использовать результат одной функции в качестве аргумента для другой функции, создавая таким образом более сложные и мощные вычисления. Например, вы можете использовать функцию SUM для суммирования значений в диапазоне ячеек, а затем использовать результат этой функции в функции COUNT для подсчета количества полученных значений.
Однако создание сложных формул с вложенными функциями может показаться сложным заданием. В этой статье мы рассмотрим пошаговое руководство по созданию сложной формулы с вложенными функциями в Excel, которое поможет вам эффективно использовать мощь этих функций и улучшить свою работу с данными.
Создание сложной формулы с вложенными функциями в Excel: пошаговое руководство
Шаг 1: Понимание задачи и определение необходимых функций
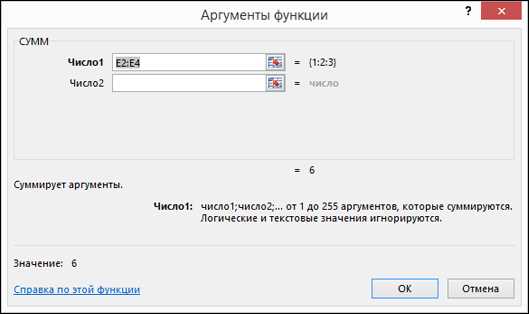

Первым шагом перед созданием сложной формулы является ясное понимание задачи, которую вы хотите решить с помощью Excel. Определите, какие конкретные вычисления вам необходимо выполнить и какие функции могут вам в этом помочь.
Рассмотрим пример. Допустим, у вас есть список с данными о продажах вашей компании за последний месяц. Вам нужно рассчитать общую сумму продаж и количество успешных сделок.
Шаг 2: Создание формулы
Теперь, когда вы определили необходимые функции, можно приступить к созданию формулы.
- Откройте Excel и выберите ячейку, в которую вы хотите поместить результат.
- Начните формулу с символа «=».
- Вводите первую функцию, необходимую для выполнения вычисления.
- Вставьте необходимые аргументы функции в скобки, используя ссылки на ячейки или значения.
- Повторите этот процесс для остальных функций, которые вы хотите включить в формулу.
- В случае необходимости используйте операторы и другие функции для выполнения дополнительных вычислений.
Шаг 3: Тестирование формулы и проверка результатов
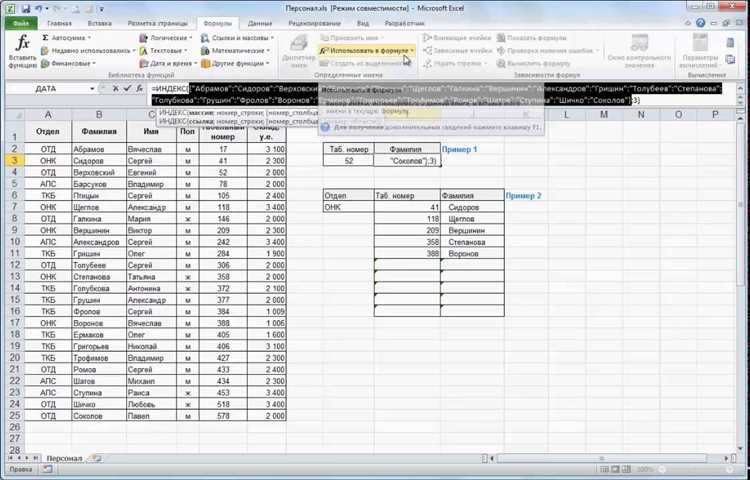

После создания формулы рекомендуется протестировать ее и проверить полученные результаты.
- Убедитесь, что все ссылки на ячейки указывают на правильные данные.
- Измените значения в ячейках, чтобы проверить, как формула реагирует на изменения данных.
- Проверьте, что результаты формулы совпадают с ожидаемыми значениями.
Обратите внимание на ошибки, которые могут возникнуть в процессе создания или тестирования формулы, и внесите соответствующие изменения, чтобы исправить их.
Определение цели формулы
При определении цели формулы необходимо учитывать конкретные задачи и требования, которые нужно решить с помощью формулы. Например, цель может быть вычисление среднего значения определенного диапазона данных, определение наибольшего или наименьшего значения, или выполнение сложной математической операции. Определение цели формулы помогает определить необходимые функции и операторы, которые нужно использовать.
Важно выделить, что определение цели формулы также помогает разбить задачу на более мелкие этапы и определить порядок выполнения операций. Это позволяет структурировать формулу и облегчить ее понимание и отладку.
Наконец, определение цели формулы также помогает установить критерии успешного выполнения задачи. Например, цель может быть достижение определенного числового значения или выполнение определенного условия. Это позволяет лучше контролировать результаты и проверять, что формула работает правильно.
Выбор основной функции
Выбор основной функции зависит от конкретной задачи, которую необходимо решить. Например, если требуется выполнить математические расчеты, может быть полезно использовать функции SUM, AVERAGE или MAX/MIN. Если нужно произвести поиск или фильтрацию данных, то подходящими функциями могут быть VLOOKUP, INDEX, MATCH или COUNTIF.
Важно выбрать функцию, которая соответствует требованиям задачи и обладает необходимыми возможностями. Также стоит учитывать, что выбранная функция может потребовать вложения других функций для достижения желаемого результата. Это может включать использование функций-агрегатов, текстовых функций, логических функций и т.д.
В конечном итоге, выбор основной функции должен быть обоснованным и соответствовать нуждам конкретной задачи. Он будет формировать основу для дальнейшего использования вложенных функций и помочь создать сложную формулу, которая эффективно выполнит требуемые действия.
Вложение дополнительных функций
В Excel есть возможность вкладывать одну функцию внутри другой, чтобы создать сложные вычислительные формулы с несколькими уровнями вложенности. Это предоставляет пользователям большую гибкость и функциональность при обработке данных.
Например, вы можете использовать функцию СУММ для суммирования диапазона ячеек, а затем вкладывать эту функцию внутри другой функции, такой как СРЕДНЕЕ, чтобы найти среднее значение суммы. Подобно тому, вы можете вкладывать функции ПРОД и СТР внутри функции ВПР для расчета выручки и налоговых выплат на основе произведения и ставки.
Вложение дополнительных функций позволяет пользователю максимально эффективно использовать возможности Excel и создавать сложные формулы, которые могут обрабатывать и анализировать данные нестандартными способами.
Задание аргументов для каждой функции
Для начала, необходимо определить, какие аргументы требуются для каждой функции в формуле. Аргументы могут быть значениями, ячейками со значениями, ссылками на другие ячейки или диапазонами ячеек. Важно учесть, что каждая функция имеет свои уникальные требования к аргументам, и необходимо соблюдать их спецификации.
При задании аргументов для каждой функции следует обратить внимание на правильную последовательность их указания. В случае, если аргументы функции имеют различные типы данных, необходимо убедиться в их совместимости и корректности использования. При несоблюдении правильной последовательности или неверном задании типов данных, формула может выдать неверный результат или ошибку.
Расстановка скобок в формуле
Правильная расстановка скобок в формуле помогает избежать ошибок и недоразумений. Важно помнить о приоритете выполнения операций в Excel, например, умножение и деление выполняются перед сложением и вычитанием. Если требуется, чтобы определенная операция была выполнена в первую очередь, ее можно заключить в отдельные скобки.
Когда в формуле используются вложенные функции, расстановка скобок становится особенно важной. Вложенные функции должны быть правильно заключены в скобки, чтобы Excel мог правильно интерпретировать их и вычислить результат. Вложенные функции могут быть различных типов, таких как математические, текстовые, статистические и т. д., и они могут быть вложены друг в друга несколько раз.
При создании сложной формулы с вложенными функциями рекомендуется использовать отступы и хорошо организованный код, чтобы облегчить чтение и понимание формулы. Четкое использование скобок поможет вам и другим пользователям легко разобраться в запутанных формулах и избежать ошибок при выполнении вычислений.
Проверка работы формулы на примерах данных
После создания сложной формулы с вложенными функциями в Excel, важно проверить ее работу на примерах данных. Это позволит убедиться, что формула правильно выполняет вычисления и возвращает ожидаемые результаты.
Для начала, можно использовать небольшой набор данных и применить формулу к каждой ячейке. Затем необходимо вручную проверить результаты, убедившись, что они соответствуют ожиданиям.
Для более обширной проверки можно использовать большие наборы данных, включающие различные комбинации значений и условий. Также стоит убедиться, что формула правильно обрабатывает все возможные случаи, включая ситуации с отсутствием данных или ошибками.
При проверке формулы на примерах данных необходимо обратить внимание на все компоненты и операторы, входящие в формулу. Проверку можно выполнить по шагам, вычисляя каждую часть формулы отдельно и сравнивая результаты с ожиданиями.
Если при проверке формулы на примерах данных возникают проблемы или несоответствия ожиданиям, необходимо внимательно рассмотреть каждую часть формулы и проверить правильность написания и логику вычислений. Возможно, потребуется внести корректировки в формулу, чтобы она работала корректно.
Вопрос-ответ:
Как проверить работу формулы на примерах данных?
Для проверки работы формулы на примерах данных можно выполнить следующие шаги: 1) Взять набор данных, который хотите использовать. 2) Применить формулу к этим данным. 3) Сравнить полученный результат с ожидаемым результатом. Если результаты совпадают, то формула работает корректно.
Какие данные следует использовать для проверки формулы?
Для проверки формулы следует использовать разнообразные данные, включая разные значения и разные комбинации значений. Важно учесть все возможные случаи и граничные условия. Это поможет выявить возможные ошибки или несоответствия в работе формулы.
Как определить ожидаемый результат при проверке формулы?
Ожидаемый результат при проверке формулы обычно определяется заранее на основе известных данных или результатов других расчетов. Если формула применяется к известным данным, можно проверить результат вручную. Если формула применяется к результатам других расчетов, то ожидаемый результат будет совпадать с этими результатами.
Что делать, если результаты проверки формулы неправильные?
Если результаты проверки формулы неправильные, необходимо внимательно проверить саму формулу на наличие ошибок. Возможно, вы сделали опечатку или неверно выбрали операторы или функции. Также стоит перепроверить входные и выходные данные на предмет соответствия форматам и требованиям формулы. Если ошибка не удается найти, можно обратиться к специалистам для получения помощи.
Есть ли способы автоматизировать проверку работы формулы на примерах данных?
Да, существуют способы автоматизировать проверку работы формулы на примерах данных. Для этого можно использовать программные средства, такие как языки программирования или специальные инструменты для тестирования. Такие средства позволяют автоматически применять формулу к набору данных и сравнивать полученный результат с ожидаемым. Это упрощает и ускоряет процесс проверки и позволяют обнаруживать ошибки или несоответствия в работе формулы.