
Расчеты и анализ данных являются важными инструментами в современном мире, особенно для бизнеса и научных исследований. Microsoft Excel предоставляет пользователю широкий функционал для работы с данными, включая возможность применять функции линейного и нелинейного регрессионного анализа.
Линейный регрессионный анализ – это метод, позволяющий найти математическую модель, которая наиболее точно описывает связь между двумя переменными. В Excel можно использовать функции, такие как TREND и LINEST, чтобы получить коэффициенты линейной регрессии, а также прогнозировать значения на основе этих коэффициентов. Этот инструмент особенно полезен при прогнозировании трендов и анализе зависимостей в данных.
Нелинейный регрессионный анализ широко применяется для аппроксимации сложных функций, которые не могут быть описаны линейной моделью. Excel предоставляет функции, такие как LOGEST и GROWTH, которые позволяют оценить параметры и построить нелинейную регрессионную модель на основе данных. Такой анализ может быть полезен при изучении процессов, которые подчиняются нелинейным законам, например, в физике или биологии.
Работа с функциями линейного и нелинейного регрессионного анализа в Microsoft Excel может быть очень полезной для тех, кто занимается анализом данных. Это позволяет проводить более точные прогнозы и извлекать информацию из сложных наборов данных. Благодаря гибкости и мощности Excel, пользователи имеют возможность настраивать различные модели и прогнозировать результаты на основе этих моделей.
Что такое линейный регрессионный анализ и зачем он нужен в Microsoft Excel
Линейный регрессионный анализ имеет широкий спектр применений. Он может быть использован для прогнозирования результатов исследований, анализа экономических данных, оценки эффективности маркетинговых кампаний и многих других задач. Благодаря встроенным функциям в Microsoft Excel, пользователи могут проводить анализ данных и строить прогнозные модели прямо в своих таблицах без необходимости использования дополнительных инструментов или программного обеспечения.
Для проведения линейного регрессионного анализа в Excel необходимо выбрать набор данных, определить зависимую переменную и одну или несколько независимых переменных. Затем нужно указать функцию регрессии, которая будет использоваться для построения модели. Excel автоматически вычислит коэффициенты регрессии и предоставит результаты анализа, включая уравнение регрессии, коэффициенты детерминации и стандартные ошибки.
Линейный регрессионный анализ в Microsoft Excel является мощным инструментом для анализа данных и прогнозирования будущих событий. Он позволяет пользователям строить простые и сложные модели, а также проводить различные статистические тесты для оценки качества моделей. Благодаря удобному интерфейсу и встроенным функциям Excel, пользователи могут быстро и точно анализировать данные и получать ценные результаты без необходимости особых навыков программирования или статистического анализа.
Создание функций для линейной регрессии в Microsoft Excel
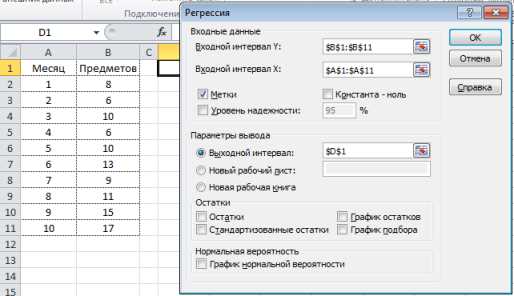
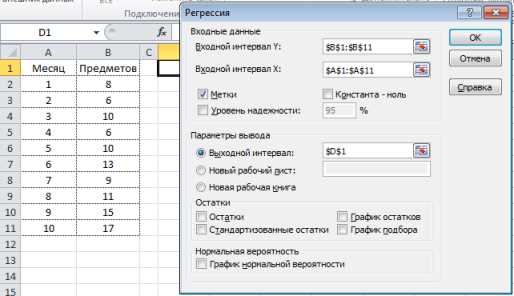
Для создания функций для линейной регрессии в Excel необходимо использовать встроенные инструменты анализа данных. Возможности анализа данных в Excel позволяют проводить линейную регрессию как для одной независимой переменной, так и для нескольких переменных одновременно. При создании функций для линейной регрессии в Excel вы можете указать диапазон ячеек, содержащих независимые и зависимые переменные, а также получить график регрессии и статистические параметры модели.
Для создания функций для линейной регрессии в Excel вам необходимо выбрать ячейку, в которой хотите получить результат, затем выбрать вкладку «Данные» и в разделе «Анализ» выбрать «Регрессия». В открывшемся окне вам нужно указать диапазон ячеек с независимыми и зависимыми переменными, выбрать опции, такие как построение графика и расчет статистики, а затем нажать «ОК». Excel автоматически создаст функцию регрессии, которую вы можете использовать для дальнейшего анализа и прогнозирования.
Нахождение коэффициентов регрессии
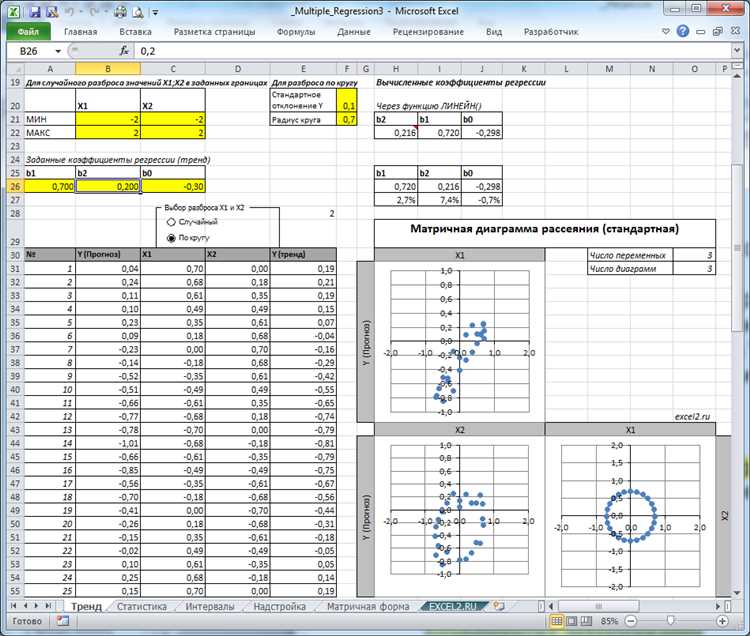

Для нахождения коэффициентов регрессии в Microsoft Excel можно использовать функцию «LINEST». Эта функция позволяет получить не только значения коэффициентов, но и другие статистические показатели, такие как стандартные ошибки коэффициентов, коэффициенты детерминации и другие.
Для использования функции «LINEST» нужно сначала создать массивы данных для зависимой переменной и независимых переменных. Затем можно использовать формулу «=LINEST(зависимая_переменная_диапазон, независимые_переменные_диапазон, TRUE, TRUE)», где вместо «зависимая_переменная_диапазон» указывается диапазон ячеек с данными для зависимой переменной, а вместо «независимые_переменные_диапазон» указывается диапазон ячеек с данными для независимых переменных. После ввода формулы, нажмите клавишу «Ctrl+Shift+Enter».
Функция «LINEST» выведет массив значений, в котором первое значение будет коэффициент наклона (или коэффициент при независимой переменной), а второе значение будет свободным членом (или коэффициентом при константе). Другие значения в массиве будут стандартными ошибками коэффициентов и другими статистическими показателями.
Предсказание значений с помощью линейной регрессии
Для использования линейной регрессии в Microsoft Excel необходимо воспользоваться соответствующей функцией. Эта функция позволяет построить линию тренда, которая проходит через имеющиеся данные и может быть использована для предсказания значений для новых наблюдений. Чтобы сделать это, необходимо указать диапазон ячеек с независимыми переменными и диапазон ячеек с зависимыми переменными.
После построения линии тренда с помощью линейной регрессии можно использовать ее для предсказания значений для новых наблюдений. Например, если у вас есть данные о доходах и расходах компании за последние несколько лет, вы можете использовать линейную регрессию для предсказания расходов на следующий год на основе доходов. Это позволит вам строить прогнозы и принимать более осознанные решения о бюджетировании и планировании.
Линейная регрессия также позволяет оценить степень влияния каждой независимой переменной на зависимую переменную. Это может быть полезно для выявления наиболее значимых факторов, влияющих на исследуемый процесс, и определения, какие переменные следует учесть при предсказании значений. Кроме того, линейная регрессия позволяет оценить точность предсказания, что позволяет судить о надежности полученных результатов.
Анализ нелинейных функций в Microsoft Excel
Для проведения анализа нелинейных функций в Microsoft Excel доступны различные инструменты и функции, которые позволяют исследовать зависимости, не поддающиеся линейному описанию. Это позволяет более точно моделировать различные явления и составлять прогнозы.
Одним из основных инструментов для анализа нелинейных функций в Excel является функция REGRESSION, которая позволяет определить нелинейную зависимость между переменными и построить соответствующую модель. С помощью этой функции можно вычислить коэффициенты нелинейной регрессии и получить показатели качества модели.
Вместе с функцией REGRESSION в Excel также доступны другие функции для анализа нелинейных зависимостей, такие как LINEST, TREND, FORECAST и др. С их помощью можно рассчитать прогнозные значения для нелинейных моделей и определить степень соответствия модели данным.
Кроме того, Microsoft Excel предоставляет возможности для визуализации и анализа нелинейных функций. С помощью графических инструментов, таких как диаграммы рассеяния и кривые тренда, можно наглядно представить нелинейные зависимости и выявить особенности данных.
Таким образом, анализ нелинейных функций в Microsoft Excel позволяет исследовать сложные зависимости и строить более точные модели для прогнозирования различных явлений. Это полезный инструмент для аналитиков, исследователей и всех, кто работает с данными и хочет получить более глубокое понимание закономерностей в данных.
Выбор подходящей модели
Первым шагом при выборе модели является анализ графика рассеяния, который позволяет визуально оценить форму зависимости между переменными. Если график демонстрирует линейную зависимость, то подходит модель линейной регрессии. В случае, если график имеет нелинейную форму, то может понадобиться использовать нелинейные модели, такие как полиномиальная регрессия или экспоненциальная регрессия.
Для проверки подходящести моделей также используется статистический анализ, включая оценку качества модели при помощи показателей, таких как коэффициент детерминации (R-квадрат) и средняя квадратическая ошибка (MSE). Эти показатели позволяют оценить, насколько хорошо модель объясняет вариацию зависимой переменной и ошибку предсказания, соответственно.
Кроме того, при выборе модели необходимо учитывать априорные знания о природе исследуемых переменных, а также учитывать возможные предположения и ограничения модели. Например, при анализе временных рядов может быть полезно использовать модели авторегрессии или скользящего среднего. Важно выбрать модель, которая лучше всего соответствует целям и предметной области исследования.
Поиск оптимальных параметров функции
Для поиска оптимальных параметров функции можно использовать различные методы, например метод наименьших квадратов или метод максимального правдоподобия. Метод наименьших квадратов основан на минимизации суммы квадратов отклонений модели от фактических значений. Метод максимального правдоподобия основан на максимизации вероятности наблюдаемых данных при заданных параметрах функции.
В Microsoft Excel для поиска оптимальных параметров функции можно использовать встроенные инструменты, такие как функция «СДВГЛ» или «Подбор параметров». Они позволяют автоматически определить значения параметров функции на основе заданных данных. При необходимости можно также использовать дополнительные средства, такие как математические пакеты программирования или специализированные программы для статистического анализа данных.
Вопрос-ответ:
Как найти оптимальные параметры функции?
Для поиска оптимальных параметров функции можно использовать различные алгоритмы оптимизации, такие как градиентный спуск, алгоритмы поиска по сетке или случайный поиск.
Что такое градиентный спуск?
Градиентный спуск — это алгоритм оптимизации, который используется для поиска локального минимума или максимума функции. Он основан на вычислении итерационного градиента функции и последующем обновлении параметров в направлении, противоположном градиенту.
Как работает алгоритм случайного поиска?
Алгоритм случайного поиска заключается в случайном выборе значений параметров функции из заданных диапазонов. Затем производится оценка целевой функции для каждой комбинации параметров. Чтобы найти оптимальные параметры, алгоритм может выполнять множество случайных выборов и сохранять лучшие значения.
Что такое алгоритмы поиска по сетке?
Алгоритмы поиска по сетке — это методы оптимизации, которые используют заранее определенную сетку значений параметров. Значение целевой функции вычисляется для каждой комбинации параметров из сетки. Алгоритм выбирает оптимальные параметры, основываясь на полученных значениях целевой функции.
Как выбрать оптимальную стратегию поиска оптимальных параметров функции?
Выбор оптимальной стратегии поиска оптимальных параметров функции зависит от характеристик самой функции и требований к точности. Некоторые функции могут иметь аналитическое решение для определения оптимальных параметров. В остальных случаях следует использовать эмпирические методы, такие как градиентный спуск, случайный поиск или алгоритмы поиска по сетке, и выбирать наилучший результат.
Что такое оптимальные параметры функции?
Оптимальные параметры функции — это набор значений, при котором функция достигает наилучшего результата или минимума/максимума определенного показателя. Определение оптимальных параметров зависит от поставленной задачи и целевой функции.
Как найти оптимальные параметры функции?
Найти оптимальные параметры функции можно с использованием методов оптимизации, таких как градиентный спуск, метод Ньютона или генетические алгоритмы. Эти методы позволяют итеративно изменять значения параметров функции с целью поиска минимума или максимума целевой функции.