
Microsoft Excel является одним из самых популярных инструментов для работы с данными и проведения различных анализов. Один из основных аспектов анализа данных — это расчет и анализ корреляций и ковариаций. Корреляция и ковариация позволяют определить наличие и степень взаимосвязи между двумя или более переменными в наборе данных.
Корреляция — это мера силы и направления линейной связи между двумя переменными. Она может принимать значения от -1 до 1, где отрицательное значение указывает на обратную связь, положительное — на прямую связь, а значение равное нулю означает отсутствие связи. Ковариация в свою очередь оценивает совместную изменчивость двух переменных.
Анализ корреляций и ковариаций в Microsoft Excel является неотъемлемой частью ряда исследований и аналитических задач. Он помогает выявить взаимосвязи в данных, определить влияние одной переменной на другую, а также помогает прогнозировать будущие значения переменных. Правильное использование этих методов с помощью Microsoft Excel может значительно облегчить анализ данных и помочь принимать более обоснованные решения на основе полученных результатов.
Зачем нужны расчет и анализ корреляций и ковариаций в Microsoft Excel?
Microsoft Excel предоставляет мощные инструменты для расчета и анализа корреляций и ковариаций, которые играют важную роль в области статистики и анализа данных.
Одной из главных причин использования этих функций является возможность выявления связей между различными переменными и определение степени их взаимосвязи. Расчет корреляции позволяет оценить, насколько тесная связь между двумя переменными, в то время как ковариация позволяет измерить степень изменчивости одной переменной по отношению к другой.
Анализ корреляций и ковариаций в Excel полезен для множества задач, включая прогнозирование, моделирование рисков, оценку эффективности стратегий и принятие взвешенных решений на основе данных.
Благодаря удобному интерфейсу и гибким возможностям Excel можно быстро провести расчеты, визуализировать результаты с помощью диаграмм и провести статистическую интерпретацию данных. Это позволяет пользователям получить ценные инсайты и принять обоснованные решения на основе статистической информации.
Инструменты для анализа данных в Excel
Кроме того, Excel также предлагает инструменты для расчета ковариации, который позволяет измерить степень, с которой две или более переменные изменяются вместе. Расчет ковариации может быть полезен для определения, зависит ли две переменные от общих факторов или нет.
В дополнение к этим инструментам, Excel имеет возможности построения графиков для визуализации данных. Графики позволяют наглядно представить взаимосвязь между переменными и выявить возможные закономерности или тренды.
С помощью этих инструментов анализа данных в Excel пользователи могут провести качественный и количественный анализ, выявить взаимосвязи и зависимости между переменными, а также принять информированные решения на основе полученных результатов.
Важность корреляций и ковариаций для анализа данных
Корреляция измеряет силу и направление связи между двумя переменными. Величина коэффициента корреляции показывает, насколько сильно переменные связаны между собой: чем ближе коэффициент к 1 или -1, тем сильнее связь. Положительная корреляция указывает на прямую связь между переменными, тогда как отрицательная корреляция указывает на обратную связь.
Ковариация, с другой стороны, измеряет направленность и силу линейной связи между двумя переменными без нормализации. Ковариация может быть положительной, отрицательной или нулевой. Положительная ковариация указывает на то, что переменные варьируются в одном направлении, тогда как отрицательная ковариация указывает на изменение переменных в противоположных направлениях.
Как рассчитать и анализировать корреляции в Microsoft Excel?
Microsoft Excel предоставляет возможность рассчитывать и анализировать корреляции между данными. Корреляция позволяет определить, насколько две или более переменных связаны друг с другом. Это важный аспект при анализе данных, так как позволяет понять, есть ли взаимозависимость между различными факторами.
Для расчета корреляций в Excel можно использовать функцию КОРРЕЛ. Данная функция вычисляет коэффициент корреляции Пирсона между двумя наборами данных. Воспользовавшись данной функцией, можно рассчитать корреляцию для любого количества переменных.
Для начала необходимо узнать адреса ячеек, содержащих данные, между которыми нужно рассчитать корреляцию. Затем нужно ввести формулу =КОРРЕЛ(диапазон1, диапазон2), указав соответствующие диапазоны данных, например, A1:A10 и B1:B10. После нажатия клавиши Enter, Excel рассчитает коэффициент корреляции для указанных диапазонов и отобразит результат в выбранной ячейке.
Для анализа корреляций в Excel также можно использовать инструменты встроенного анализа данных. Например, с помощью инструмента «Анализ регрессии» можно рассчитывать корреляцию для нескольких переменных одновременно и строить графики для их визуализации. Данные инструменты позволяют проводить более глубокий и детальный анализ корреляций между различными факторами.
Использование функции КОРР
Функция КОРР обладает простым синтаксисом и требует только указания двух аргументов — диапазона ячеек, содержащих первый набор данных, и диапазона ячеек, содержащих второй набор данных. Результатом функции будет число от -1 до 1: значение ближе к 1 указывает на положительную корреляцию, ближе к -1 — на отрицательную, а значение около нуля свидетельствует о слабой или отсутствующей связи между переменными.
Применение функции КОРР позволяет проводить анализ данных и выявлять зависимости между ними. Это особенно полезно при исследовании социальных, экономических и финансовых показателей, где важно определить наличие или отсутствие взаимосвязей между различными переменными. Коэффициент корреляции, полученный с помощью функции КОРР, может помочь в планировании бизнес-стратегий и принятии важных решений на основе анализа данных.
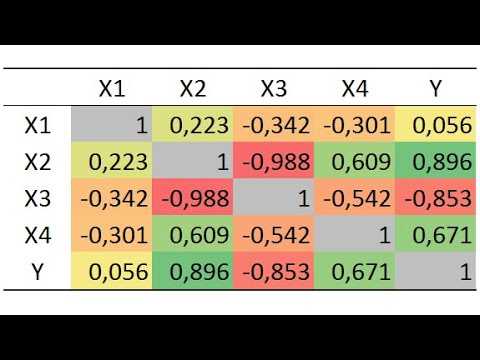
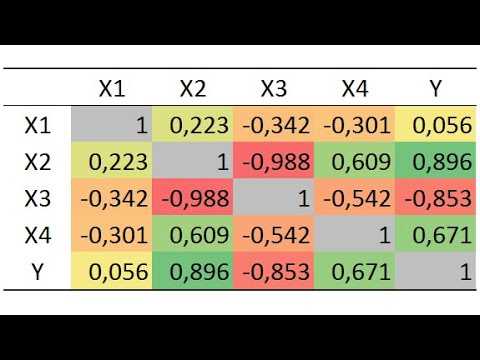
Интерпретация результатов корреляционного анализа
Корреляционный анализ позволяет оценить подобие или различие между двумя переменными. При интерпретации результатов корреляционного анализа необходимо учитывать коэффициент корреляции, его значение и ориентировочную силу связи.
Коэффициент корреляции может принимать значения от -1 до 1. Знак коэффициента указывает на направление связи между переменными: положительный коэффициент говорит о прямой связи, а отрицательный — о обратной связи. Чем ближе значение коэффициента к 1 или -1, тем более сильная связь между переменными.
Например, если коэффициент корреляции равен 0, это может указывать на отсутствие связи между переменными. В то время как значение 0,5 или -0,5 может свидетельствовать о умеренной связи. Значения, близкие к 1 или -1 (например, 0,8 или -0,8), указывают на сильную связь между переменными.
Помимо значения коэффициента корреляции, важно также учитывать область применения и особенности исследования при интерпретации результатов. Например, если данные получены в ограниченной выборке или имеют сезонные колебания, это может повлиять на значимость связи между переменными.
Рассчет и анализ ковариаций в Microsoft Excel
Для начала необходимо выбрать два набора данных, между которыми нужно определить ковариацию. Затем воспользуйтесь формулой COVAR, указав в качестве аргументов диапазоны соответствующих ячеек с данными. Результатом будет числовое значение, показывающее силу связи между переменными – положительные значения указывают на прямую взаимосвязь, отрицательные – на обратную.
Кроме рассчета ковариации, можно провести анализ полученных данных. Для этого помимо простого числового значения ковариации можно использовать графическое представление данных в виде диаграммы рассеяния. Это позволит визуализировать взаимосвязь между переменными и получить дополнительное представление о характере связи. Также можно использовать коэффициент корреляции, который показывает не только наличие связи, но и ее степень – он всегда находится в диапазоне от -1 до 1. Близкие к 1 значения указывают на сильную положительную взаимосвязь, близкие к -1 – на сильную отрицательную, а значения около нуля – на отсутствие взаимосвязи.
Использование функции СОВАР
Функция СОВАР в Excel используется для расчета ковариации между двумя рядами данных. Это позволяет определить, насколько две переменные изменяются вместе.
Эта функция принимает два аргумента: первый аргумент представляет собой диапазон значений первого ряда данных, а второй аргумент — диапазон значений второго ряда данных. Функция СОВАР возвращает ковариацию между этими двумя рядами данных.
Ковариация может принимать положительные и отрицательные значения. Если ковариация положительна, это означает, что две переменные имеют положительную линейную связь и изменяются вместе. Если ковариация отрицательна, это означает, что две переменные имеют отрицательную линейную связь и меняются в противоположных направлениях. Если ковариация равна нулю, это означает, что между переменными нет линейной связи.
Функция СОВАР может быть полезна при анализе данных и определении взаимосвязи между различными переменными. Например, она может помочь выявить, есть ли зависимость между доходом и расходами, показать, как одна переменная влияет на другую или насколько сильно две переменные коррелируют между собой.
Вопрос-ответ:
Что такое функция СОВАР?
Функция СОВАР (СОвместный ВАРиант) — это специальная функция в эконометрике, используемая для оценки рисков при прогнозировании временных рядов. Она позволяет учесть зависимости между различными вариантами развития событий и получить более точные прогнозы.
Как работает функция СОВАР?
Функция СОВАР основана на моделировании множества возможных сценариев развития событий и учете зависимостей между ними. Она использует методы статистического анализа и прогнозирования для оценки вероятностей различных исходов и их последствий.
Какие преимущества имеет использование функции СОВАР?
Использование функции СОВАР позволяет учесть зависимости и взаимосвязи между различными вариантами развития событий, что позволяет получить более точные и надежные прогнозы. Это особенно полезно при прогнозировании рисков и принятии стратегических решений.
В каких областях применяется функция СОВАР?
Функция СОВАР применяется в различных областях, где требуется прогнозирование и учет рисков. Она находит широкое применение в экономике, финансах, управлении проектами, страховании и других областях, где важно оценить вероятности различных сценариев развития.
Как можно использовать функцию СОВАР в анализе временных рядов?
Функция СОВАР может быть использована для прогнозирования временных рядов, учета стохастических зависимостей и расчета вероятностей различных исходов. Она позволяет оценить вероятности различных сценариев развития и оценить риски, связанные с прогнозируемыми данными.