
Анализ связей и зависимостей между различными переменными является неотъемлемой частью процесса анализа данных. Важно понимать, какие факторы влияют на определенную переменную и до какой степени. Регрессионный анализ в Microsoft Excel — мощный инструмент, который позволяет исследовать эти связи и строить прогнозы на основе имеющихся данных.
Основной идеей регрессионного анализа является представление зависимой переменной как функции независимых переменных. Это позволяет оценить влияние каждого фактора на исследуемую переменную и определить степень зависимости. В Microsoft Excel доступны различные инструменты для выполнения регрессионного анализа, включая встроенные функции и инструменты анализа данных.
Начиная работу с регрессионным анализом в Microsoft Excel, необходимо подготовить данные и определить зависимую и независимые переменные. Затем можно использовать функцию регрессионного анализа для построения модели и получения результатов. Важно учитывать, что регрессионный анализ представляет только статистическую связь между переменными и не дает нам понимания причинно-следственных связей.
Регрессионный анализ в Microsoft Excel может быть полезным инструментом для исследования связей и зависимостей в данных. Он позволяет оценить влияние различных факторов на определенную переменную и построить модель, которая может использоваться для прогнозирования и определения трендов. Важно помнить, что результаты регрессионного анализа должны быть тщательно интерпретированы и необходимо учесть другие влияющие факторы, которые могут оказывать влияние на исследуемую переменную.
Анализ связей и зависимостей в данных с помощью регрессионного анализа в Microsoft Excel
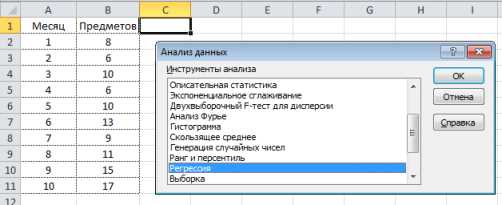

Процесс регрессионного анализа включает несколько шагов. В первую очередь, необходимо собрать данные для анализа, определить, какие переменные представляют интерес, и записать их в таблицу Excel. Затем следует построить диаграмму рассеяния, чтобы визуально оценить наличие связи между переменными. После этого можно приступить к самому анализу с помощью функции регрессии в Excel. Эта функция позволяет вычислить коэффициенты регрессии и определить статистическую значимость связей.
Регрессионный анализ в Excel также позволяет проводить дополнительные статистические тесты, такие как анализ остатков и проверка наличия мультиколлинеарности. Остатки позволяют оценить, насколько хорошо уравнение регрессии описывает данные, а мультиколлинеарность указывает на наличие корреляции между независимыми переменными. Эти дополнительные анализы помогают более полно понять связи и зависимости в данных.
Регрессионный анализ в Microsoft Excel является мощным инструментом для анализа данных и выявления связей и зависимостей. Его использование позволяет принимать обоснованные решения на основе данных и заложить основу для прогнозирования будущих результатов. Регрессионный анализ в Excel — это не только удобный, но и доступный инструмент для исследований и аналитики в различных областях, от маркетинга до науки о данных.
Что такое регрессионный анализ?
В регрессионном анализе проводится подробное изучение влияния каждой независимой переменной на зависимую переменную и определяется, насколько сильно эту зависимость можно оценить. Также регрессионный анализ позволяет определить, какие независимые переменные наиболее значимо влияют на зависимую переменную.
Для проведения регрессионного анализа в Microsoft Excel необходимо иметь набор данных, который включает значения зависимой переменной и независимых переменных. По мере добавления независимых переменных, можно определить, как каждая из них влияет на зависимую переменную и как они взаимосвязаны друг с другом.
Регрессионный анализ может быть полезен в различных областях, таких как экономика, финансы, маркетинг, социология и т.д. Он может помочь исследователям и аналитикам понять причинно-следственные связи между переменными и сделать предсказания о будущих событиях на основе имеющихся данных.
Инструменты регрессионного анализа в Microsoft Excel
Регрессионный анализ представляет собой мощный инструмент для изучения связей и зависимостей в данных. В Microsoft Excel для проведения регрессионного анализа доступны особые функции и инструменты, которые позволяют с легкостью провести расчеты и установить взаимосвязи между переменными.
Один из основных инструментов для регрессионного анализа в Microsoft Excel — это функция «Линейная регрессия». Эта функция позволяет провести анализ зависимости одной переменной от другой на основе математической модели линейной регрессии. С помощью этой функции можно определить коэффициенты регрессии, коэффициент детерминации и провести прогнозные расчеты.
Кроме того, в Microsoft Excel доступны и другие инструменты для регрессионного анализа, такие как графики регрессии и диаграммы рассеяния. Графики регрессии позволяют визуализировать зависимость между переменными, а диаграммы рассеяния помогают выявить возможные выбросы или аномалии в данных.
Как подготовить данные для регрессионного анализа?
Первым шагом при подготовке данных для регрессионного анализа является проверка на пропущенные значения. Необходимо убедиться, что все переменные, которые будут использоваться в модели, заполнены без пропусков. Если в данных присутствуют пропущенные значения, их можно удалить или заполнить средними или медианными значениями в зависимости от характера анализируемой переменной.
Далее следует провести анализ выбросов. Возможные выбросы в данных могут исказить результаты регрессионного анализа, поэтому необходимо их идентифицировать и решить, что с ними делать. Выбросы можно удалить из данных, если они являются ошибками или аномалиями, или оставить их, если они имеют особую значимость в исследовании.
Также важным шагом при подготовке данных для регрессионного анализа является преобразование переменных. Некоторые переменные могут требовать преобразования для достижения линейной зависимости с зависимой переменной. Например, возможно потребуется прологарифмировать переменные или создать новые переменные на основе существующих.
В итоге, подготовка данных для регрессионного анализа требует тщательности и систематичности. Очистка от пропущенных значений и выбросов, а также преобразование переменных позволяют получить более точные и интерпретируемые результаты в процессе анализа связей и зависимостей в данных.
Как провести регрессионный анализ в Microsoft Excel?
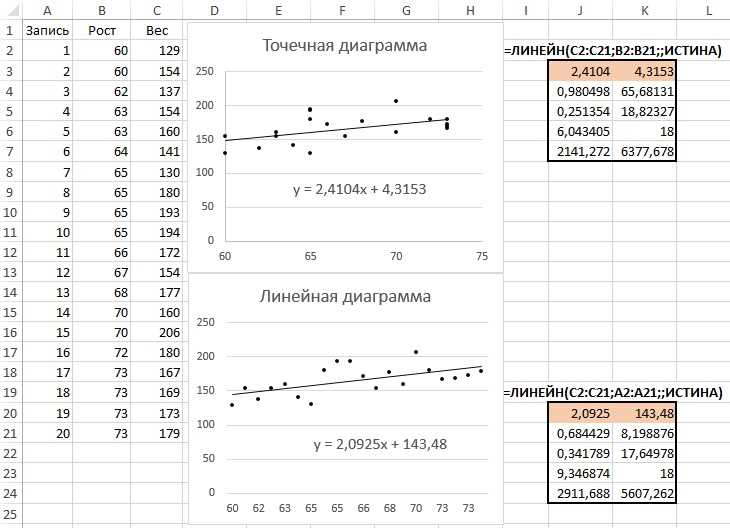

Для проведения регрессионного анализа в Microsoft Excel необходимо загрузить данные и затем выбрать соответствующие функции. Во-первых, можно использовать функцию «Регр. анализ» во вкладке «Данные», чтобы создать регрессионную модель и получить результаты анализа. Во-вторых, можно использовать функцию «Линейная регрессия» во вкладке «Статистика», чтобы получить подробную информацию о связи между переменными и коэффициентах регрессии. В-третьих, можно использовать функции «Тренд» или «Тренд.Линейный» для создания линейной модели и получения прогнозов.
В процессе проведения регрессионного анализа нужно обращать внимание на коэффициенты регрессии, такие как коэффициенты наклона (slope) и точки пересечения (intercept), которые описывают характер и степень влияния независимой переменной на зависимую переменную. Также стоит учитывать статистические показатели, такие как коэффициент детерминации (R-квадрат), который показывает, на сколько процентов изменения зависимой переменной объясняются изменениями независимой переменной.
Как интерпретировать результаты регрессионного анализа?
Вторым шагом в интерпретации результатов регрессионного анализа является анализ коэффициентов регрессии. Коэффициенты регрессии показывают величину и направление связи между независимой и зависимой переменными. Положительные коэффициенты указывают на прямую пропорциональность, то есть увеличение значения независимой переменной сопровождается увеличением значения зависимой переменной. Отрицательные коэффициенты указывают на обратную пропорциональность, то есть увеличение значения независимой переменной сопровождается уменьшением значения зависимой переменной.
Кроме того, интерпретация регрессионного анализа включает анализ статистических метрик, таких как коэффициент детерминации (R-квадрат) и стандартная ошибка регрессии. Коэффициент детерминации указывает на долю вариации зависимой переменной, которая может быть объяснена независимыми переменными. Чем ближе значение коэффициента детерминации к 1, тем лучше модель объясняет вариацию зависимой переменной. Стандартная ошибка регрессии показывает, насколько точно значения зависимой переменной могут быть предсказаны на основе независимых переменных.
Пример интерпретации результатов регрессионного анализа:
В результате регрессионного анализа была установлена статистически значимая положительная связь между количеством часов, проведенных на подготовку, и результатами студентов на экзамене (p-значение < 0.05). Коэффициент регрессии составил 0.67, что означает, что каждый дополнительный час, потраченный на подготовку, приведет к увеличению результатов на 0.67 балла. Коэффициент детерминации составил 0.55, что говорит о том, что 55% вариации результатов на экзамене может быть объяснено количеством часов, проведенных на подготовку.
Примеры применения регрессионного анализа в реальной жизни
Один из примеров применения регрессионного анализа может быть в области экономики. Например, исследователи могут использовать регрессионный анализ для выявления взаимосвязей между уровнем безработицы и уровнем экономического роста в определенной стране. Это помогает экономистам понять, как изменения в одной переменной могут влиять на другую и принять соответствующие меры для улучшения экономической ситуации.
Еще один пример применения регрессионного анализа может быть в маркетинге. Компании могут использовать регрессионный анализ для определения связи между объемом рекламных затрат и уровнем продаж. Это позволяет им оценить эффективность своей рекламной кампании и принять решения об оптимизации рекламного бюджета.
Регрессионный анализ также может быть полезен в медицине. Например, исследователи могут использовать его для определения связи между факторами риска, такими как курение, питание и уровень физической активности, и развитием сердечно-сосудистых заболеваний. Это позволяет разработать рекомендации по предотвращению развития этих заболеваний на основе влияния этих факторов.
Вопрос-ответ:
Каким образом регрессионный анализ применяется в экономике?
Регрессионный анализ широко используется в экономических исследованиях для анализа взаимосвязей между различными переменными. Например, можно провести регрессионный анализ для определения влияния уровня инфляции на экономический рост или для прогнозирования спроса на определенный товар.
В каких областях медицины используется регрессионный анализ?
Регрессионный анализ может быть использован в медицинских исследованиях для определения связи между различными факторами и заболеваемостью. Например, можно провести регрессионный анализ для выявления влияния возраста, пола и образа жизни на вероятность развития определенного заболевания.
Как можно применить регрессионный анализ в маркетинге?
В маркетинге регрессионный анализ позволяет определить влияние различных факторов на продажи товара или услуги. Например, можно провести регрессионный анализ для выявления зависимости между ценой товара, количеством рекламы и объемом продаж.
Как регрессионный анализ применяется в социологии?
Социологи могут использовать регрессионный анализ для изучения влияния различных факторов на социальные явления. Например, можно провести регрессионный анализ для определения влияния образования, дохода и места проживания на политические предпочтения определенной группы людей.
Каким образом регрессионный анализ применяется в физических науках?
В физических науках регрессионный анализ может быть использован для моделирования и прогнозирования физических процессов. Например, можно провести регрессионный анализ для определения зависимости между временем и расстоянием в свободном падении тела или для предсказания тепловых характеристик материалов.