
Microsoft Excel — это программное обеспечение, которое предоставляет возможность удобного и эффективного расчета статистических параметров. Одним из основных инструментов для выполнения этих расчетов являются операторы в формулах, которые позволяют пользователю осуществлять различные вычисления и обрабатывать данные.
Один из наиболее часто используемых статистических параметров — это среднее значение. Среднее значение вычисляется как сумма всех значений в наборе данных, деленная на количество этих значений. В Excel среднее значение можно рассчитать с помощью оператора «СРЗНАЧ», который применяется к диапазону ячеек с данными. Например, чтобы вычислить среднее значение чисел в диапазоне от A1 до A10, необходимо ввести формулу «=СРЗНАЧ(A1:A10)».
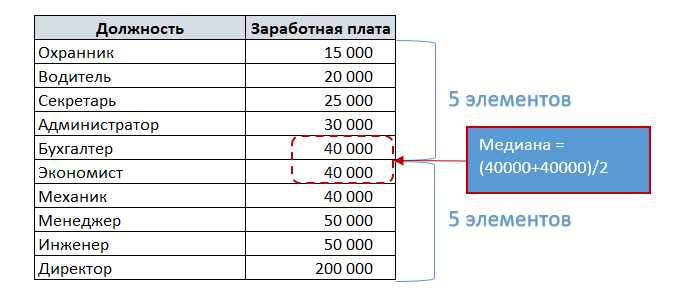
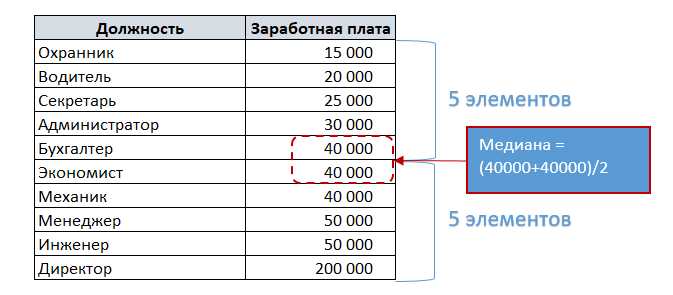
Еще один полезный статистический параметр — это медиана. Медиана представляет собой значение, которое делит упорядоченный набор данных на две равные части. Для вычисления медианы в Excel можно использовать оператор «МЕДИАН», который также применяется к диапазону ячеек с данными. Например, чтобы найти медиану чисел в диапазоне от A1 до A10, необходимо ввести формулу «=МЕДИАН(A1:A10)».
Наконец, мода — это значение, которое наиболее часто встречается в наборе данных. В Excel моду можно рассчитать с помощью оператора «ЗНАЧ.МОДА», который также применяется к диапазону ячеек с данными. Например, чтобы найти моду чисел в диапазоне от A1 до A10, необходимо ввести формулу «=ЗНАЧ.МОДА(A1:A10)».
Таким образом, с использованием операторов в формулах Microsoft Excel можно удобно рассчитывать статистические параметры, такие как среднее значение, медиана и мода. Эти параметры являются важными инструментами при анализе и интерпретации данных, и Excel предоставляет простой и эффективный способ их расчета.
Расчет статистических параметров с использованием операторов в формулах Microsoft Excel: средние значения, медиана, мода
Вторым важным параметром является медиана, которая определяет центральное значение в упорядоченном наборе данных. Расчет медианы в Excel выполняется с использованием оператора MEDIAN, который находит значение, находящееся посередине отсортированного списка чисел. Если количество чисел нечетное, медиана – это значение в середине списка, если количество чисел четное, медиана – это среднее арифметическое двух центральных чисел.
Третьим статистическим параметром является мода, которая определяет значение, которое наиболее часто встречается в наборе данных. Для расчета моды в Excel используется оператор MODE, который анализирует набор чисел и находит значение с наибольшей частотой встречаемости. Если в наборе данных нет уникального модального значения, Excel выведет сообщение о том, что мода не определена.
Статистические параметры и их роль в анализе данных
Один из основных статистических параметров — среднее значение, показывает среднюю величину набора данных и является одним из наиболее распространенных показателей центральной тенденции. Оно вычисляется путем суммирования всех значений и деления на их количество. Среднее значение помогает оценить общую тенденцию данных и получить представление о типичных значений.
Еще один важный статистический параметр — медиана. Он представляет собой значение, которое разделяет упорядоченный список данных на две равные части. Медиана полезна в случаях, когда данные содержат выбросы или являются скошенными, так как она не чувствительна к экстремальным значениям и лучше отражает типичную ситуацию.
Еще один статистический параметр, используемый в анализе данных, — мода. Мода представляет собой наиболее часто встречающееся значение в наборе данных. Она может быть полезна для идентификации наиболее популярных или характерных значений и может быть особенно полезна в случаях, когда данные имеют дискретное распределение.
В итоге, статистические параметры позволяют получить общее представление о данных и провести первичный анализ. Они могут помочь выявить паттерны, тенденции и особенности распределения данных, что в свою очередь может повысить качество принимаемых решений и помочь в прогнозировании будущих событий.
Примеры использования операторов в формулах Microsoft Excel для расчета средних значений
Операторы в формулах Microsoft Excel позволяют производить расчеты и анализировать данные с помощью различных функций. Для расчета средних значений можно использовать оператор «СРЕДНЕЕ», который позволяет найти среднее арифметическое значение набора чисел.
Пример использования оператора «СРЕДНЕЕ» в формуле: =СРЕДНЕЕ(A1:A5)
В данном примере формула вычисляет среднее арифметическое значение чисел, расположенных в диапазоне ячеек от A1 до A5. Оператор «СРЕДНЕЕ» автоматически исключает пустые ячейки и текстовые значения при расчете среднего значения.
Кроме того, операторы в формулах Microsoft Excel позволяют работать с условиями. Например, можно использовать оператор «СРЕДНЕЕЕСЛИ», чтобы вычислить среднее значение только для тех ячеек, которые удовлетворяют определенному условию. Пример использования данного оператора: =СРЕДНЕЕЕСЛИ(A1:A10, «>10»)
В этом примере формула вычисляет среднее значение только для тех ячеек в диапазоне от A1 до A10, которые содержат числа больше 10. Оператор «СРЕДНЕЕЕСЛИ» позволяет задать условие и автоматически исключает ячейки, не удовлетворяющие этому условию, из расчета среднего значения.
Как вычислить медиану с помощью операторов в формулах Microsoft Excel
Для вычисления медианы в Microsoft Excel можно использовать функцию MEDIAN. Эта функция принимает аргументы, которые представляют собой набор данных, для которого нужно найти медиану. В формуле можно указать диапазон ячеек, содержащих данные, или перечислить значения вручную, разделяя их запятыми.
После указания нужных аргументов, функция MEDIAN вычисляет медиану и возвращает ее значение. Например, если у вас есть набор данных в диапазоне ячеек A1:A10, то формула для вычисления медианы будет выглядеть следующим образом: =MEDIAN(A1:A10). После ввода этой формулы и нажатия Enter, Excel вычислит медиану для указанного набора данных.
Использование операторов для определения моды в Microsoft Excel
Один из способов определить моду в Excel — использование функции «ПОИСКПОВТ». Эта функция ищет повторяющиеся значения в диапазоне и возвращает наиболее часто встречающееся значение. Для использования данной функции необходимо указать диапазон данных, в котором необходимо найти моду.
Пример формулы для определения моды с использованием функции «ПОИСКПОВТ»:
=ПОИСКПОВТ(диапазон_данных)
Также можно использовать другие операторы, такие как «СЧЁТЕСЛИ», для определения моды. Данный оператор позволяет подсчитать количество повторяющихся значений в диапазоне данных и вернуть наиболее часто встречающееся значение. Для использования данного оператора необходимо указать диапазон данных и условие, по которому необходимо подсчитать повторяющиеся значения.
Пример формулы для определения моды с использованием оператора «СЧЁТЕСЛИ»:
=ИНДЕКС(диапазон_данных;СЧЁТЕСЛИ(диапазон_данных;диапазон_условия);0)
Использование операторов в формулах Microsoft Excel для определения моды позволяет анализировать и выявлять наиболее часто встречающиеся значения в наборе данных, что может быть полезно при анализе статистических параметров.
Типичные проблемы и ошибки при расчете статистических параметров
Одной из распространенных проблем является неправильное понимание и использование формул. Некорректно написанная или неправильно примененная формула может привести к ошибке в расчете статистических параметров. Это может быть вызвано отсутствием знания о синтаксисе формул или неправильным использованием операторов.
- Неоправданное искажение результатов может произойти из-за неверного выбора функции. Например, применение функции среднего значения на наборе данных с выбросами может привести к искажению результата.
- Незнание правил округления также является распространенной проблемой. Неправильное округление может привести к искажению результатов, особенно при расчете среднего значения.
- Пропуск значений или некорректная обработка пропущенных данных также может привести к ошибкам. Если данные содержат пропуски или некорректные значения, необходимо правильно обработать эти ситуации для получения достоверных результатов.
Для избежания вышеуказанных проблем и ошибок при расчете статистических параметров необходимо внимательно изучить синтаксис и особенности использования формул в Microsoft Excel. Также стоит уделить внимание правилам округления и обработке пропущенных данных. Правильное понимание и использование всех этих аспектов помогут получить точные и достоверные результаты при расчете статистических параметров.
Вопрос-ответ:
Какие проблемы могут возникнуть при расчете среднего значения выборки?
Одной из проблем при расчете среднего значения выборки может быть неправильное определение выборки. Если выборка содержит выбросы или не является представительной, то среднее значение может быть искажено.
В чем может заключаться ошибка при расчете дисперсии выборки?
Одной из ошибок при расчете дисперсии выборки может быть неправильное определение размаха выборки. Если размах выборки определен неправильно, то дисперсия может быть неадекватной и не отражать действительное распределение данных.
Какие трудности могут возникнуть при расчете медианы выборки?
При расчете медианы выборки может возникнуть проблема из-за наличия выбросов, особенно в случае, когда выборка содержит неравномерно распределенные значения. В таких случаях медиана может не отражать среднее значение выборки.
Какими ошибками можно допуститься при расчете стандартного отклонения выборки?
Один из распространенных ошибок при расчете стандартного отклонения выборки — неправильное определение дисперсии. Если дисперсия выборки определена неправильно, то стандартное отклонение может быть неверным и не отразить действительное распределение данных.
Какую проблему можно решить при расчете интерквартильного размаха выборки?
Один из способов решить проблему выбросов в выборке — использовать интерквартильный размах. Этот параметр позволяет определить разницу между верхним и нижним квартилями и исключить выбросы, которые могут исказить оценку центральной тенденции выборки.